Crystal Lattices ( The Solid State Notes )
- Crystalline solids have a regular and periodically repeating pattern of constituent particles.
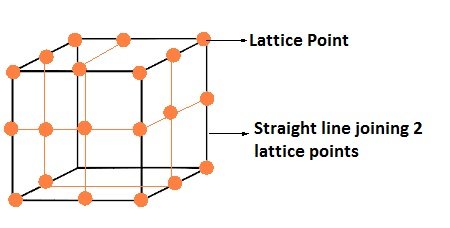
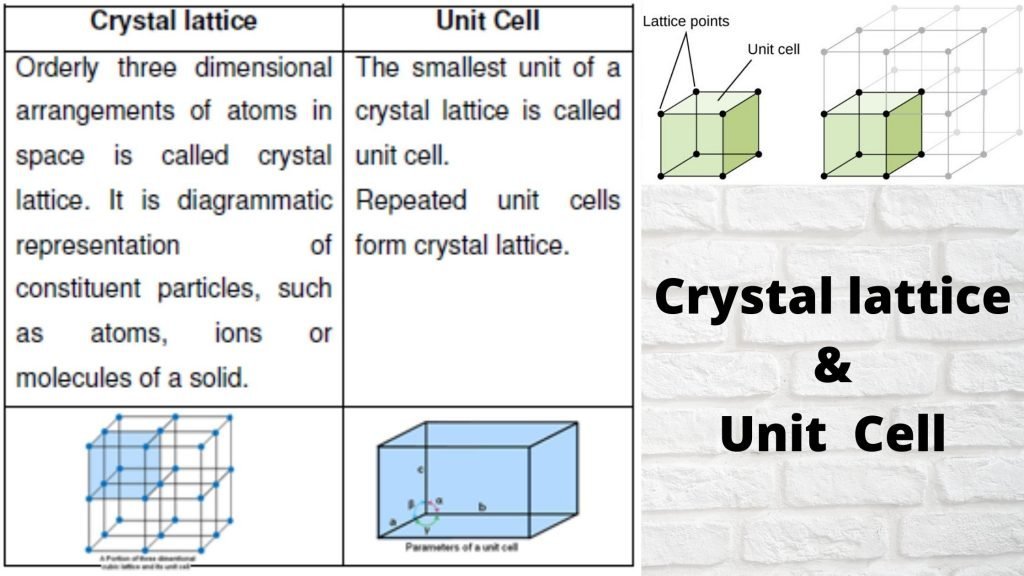
- The diagrammatical representation of three dimensional arrangements of constituent particles of a crystal in space with each particle depicted as a point is called crystal lattice.
- There are only 14 possible three dimensional lattices and are known Bravais Lattices.
- Each point in a lattice is called lattice point or lattice site.
- Each point in a crystal lattice signifies one constituent particle which can be an atom, a molecule or an ion.
- Lattice points are joined together using straight lines to identify the geometry of the lattice.
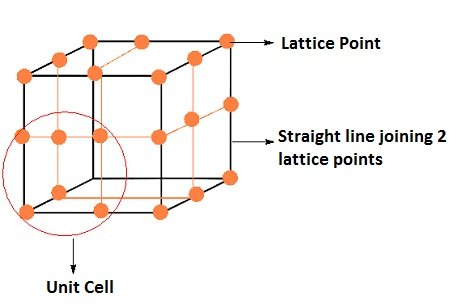
Unit Cells ( The Solid State Notes )
Unit cell can be described as the smallest portion of a crystal lattice.
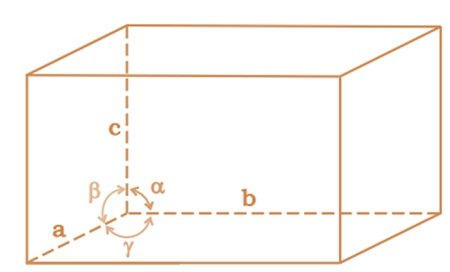
A unit cell is characterized by:
(i) Its dimensions along the three edges, a, b and c which may or may not be mutually perpendicular.
- Angles between the edges, α (between b and c) β (between and c) and γ (between a and b). Thus, a unit cell is characterized by six parameters a, b, c, α, β and γ.
Crystal Lattice & Unit Cell :-
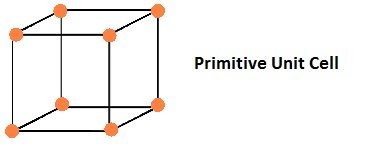
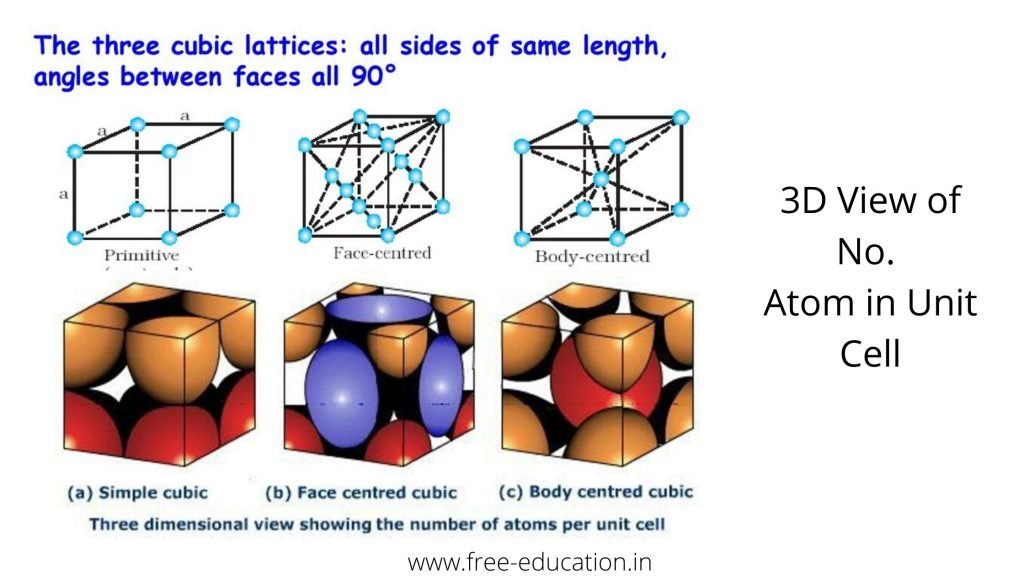
Primitive Unit Cells
If the constituent particles of a crystal lattice are present only on the corner positions of a unit cell, it is known as primitive unit cell.
Centered Unit Cells
- If the constituent particles of a crystal lattice are present at positions other than corners in addition to those at corners, it is known as centered unit cell.
- Centered unit cells are of three types:
- Body-Centred Unit Cells:
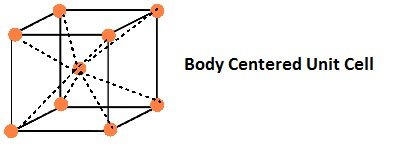
If the constituent particles of a unit cell are present at its body-centre besides the ones that are at its corners.
- Face-Centred Unit Cells:
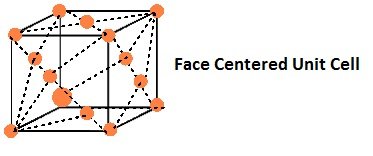
If the constituent particles of a unit cell are present at the center of each face, besides the ones that are at its corners.
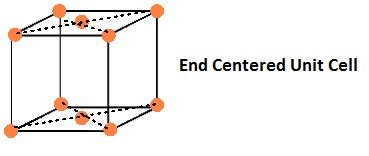
If the constituent particles of a unit cell are present the center of any two opposite faces besides the ones present at its corners.
14 Bravais Unit Cell:-

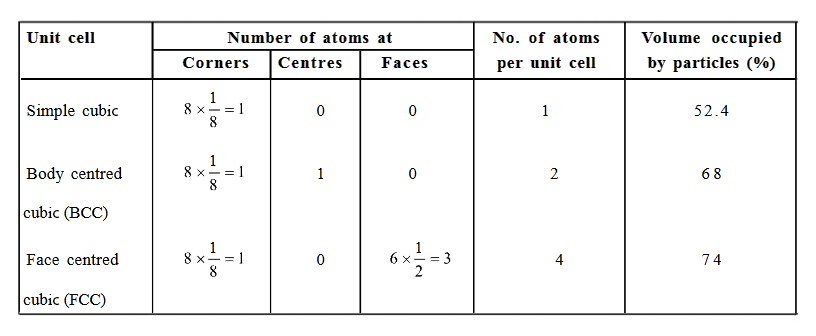
No. Atoms in Unit Cell :-
Number of atoms per unit cell : Body Centered Cubic Unit Cell
In a body-centered cubic (bcc) unit cell, the atoms are present in the body-center besides the ones that are at its corners that wholly belongs to the unit cell in which it is present. Thus in a body-centered cubic (bcc) unit cell:
8 corners X 1/8 per corner atom = 8 * 1/8 = 1 atom
1 body center atom = 1 X 1 = 1 atom
Total number of atoms per unit cell = 2 atoms
Question: Niobium crystallises in body-centred cubic structure. If density is 8.55 g cm-3, calculate atomic radius of niobium using its atomic mass 93 u.
Answer: Density = 8.55 gcm-3
Consider length of the edge = a cm
Number of atoms per unit cell, Z = 2
M = 93 u
Using the formula

Number of atoms per unit cell : Face Centered Cubic Unit Cell
- In a face-centered cubic (fcc) unit cell the atoms are present in the corners and at the center of all the faces of the cube.
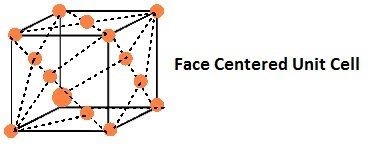
Each atom present at the face-center is shared between two adjacent unit cells and only a ½ of each atom belongs to a unit cell.
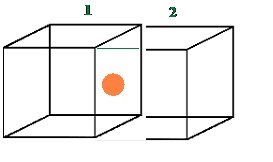
Thus, in a face-centered cubic (fcc) unit cell:
8 corners X 1/8 per corner atom = 8 * 1/8 = 1 atom
6 face-centered atoms X 1/2 per unit cell = 6 X 1/2 = 3 atoms
Total number of atoms per unit cell = 4 atoms
In solids, these constituent particles are closely-packed that leaves minimum vacant space.
Question : An element with molar mass 2.7×10-2kg mol-1 forms a cubic unit cell with edge length 405 pm. If its density is 2.7×103kg-3, what is the nature of the cubic unit cell?
Answer : d = 2.7×103kg-3
M = 2.7×10 –2 kg mol-1
a= 405 pm = 405 X 10-12
NA= 6.023 X 1023
Using the formula

Z=4
Unit cell is fcc unit cell.
Volume of 54 g of the element = 0.054/(2.7X103) = 2 X 10-6
Number of unit cell in this volume = volume of 554 g of element/volume of each unit cell = 2 X 10-6/(405 X 10-12)3 = 3.012 X 1022
Question: Copper crystallises into a fcc lattice with edge length 3.61 x 10-8cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm-3
Answer: Given that Copper crystallises into a fcc lattice
Hence Z= 4
M = 63.5
a = 3.61×10-8
No = 6.023 x 1023
Using the formula
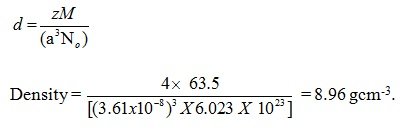
Therefore, approximately the value is equal to 8.92.
Numerical on Packing efficiency:- ( The Solid State Notes )
For this refers Chemistry book

Mohd. Sharif Qualification: B.Tech (Mechanical Engineering) [Founder of Wisdom Academy] [Aim Foundation & Free-Education.In] [Engineer By Profession | Teacher By Choice] [Blogger, YouTube Creator]






